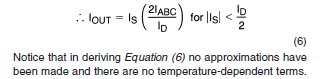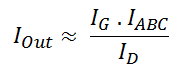-
LM13700 OTA – The missing forumla
Posted on August 15th, 2012 No commentsIf you do anything with analogue syths you quickly run in to the Operational Transconductance Amplifier (OTA) as a key component. These are amps whose current output depends on the voltage difference at the inputs and a control current that scales the gain. They are used for voltage controlled filters, voltage controlled amplifiers and oscillators. The subject of OTAs has a complicated and initially frightening set of assumptions, concepts and implicit ideas around it and getting a handle on the whole thing takes some effort. This blog post isn’t a general introduction to OTAs but it talks about how I solved a particular problem in my understanding and spotted a mistake in one of the common write-ups.
Digital techniques are replacing a lot of OTA applications and OTA chips are being discontinued like there is no tomorrow. One that is still available (and I use in the LushOne) is the venerable LM13700. While designing a voltage controlled amplifier and ring-modulator for the LushOne I found I needed to get a deeper understanding of the LM13700 than I had had before and started to explore the behaviour of the chip in detail. In particular I wanted to be able to predict the gain when the linearization diodes are in use.
The obvious place to turn is the LM13700 data sheet. This is kind-of famous because the designers tried to pack a lot of information and examples of their great new device in but the commercial pressures meant the datasheet needed to be kept short. It is therefore rather compactly written and understanding the example circuits is often an exercise for the reader. Initially though the case I was interested in seemed simple enough. The data sheet provides a nice equation with the glowing claim “no approximations have been made”.
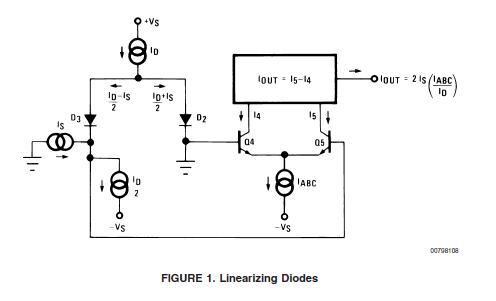
What do all the terms mean? IABC is the amp bias current (pin 1 or 16). ID is the diode bias current (pin 2 or 15). What is IS though? Fortunately Figure 1 of the data sheet tries to tell you – IS is the current being injected in to one input of the amplifier while the other input is grounded. So it all looks nice and simple – except that on the bench the gain I got was about half what I would have expected from this forumulat. In other words the figure of 2 in the numerator seems wrong! Getting to the bottom of this involved a lot of head-scratching and measuring and simulation. Once there the answer is obvious, but at the time it was a big mystery.
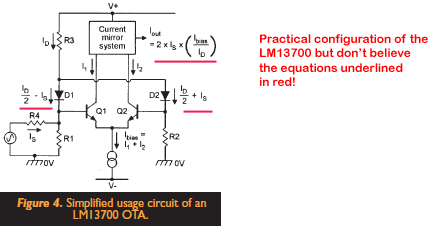
I should say at this point that the LM13700 datasheet is absolutely technically correct, but it is rather easy to misunderstand if you don’t apply your brain sufficiently. The problem lies in the interpretation of IS in a real configuration. Normal configuration (and I think any practical use of the LM13700) doesn’t use current sources to set IS and ID/2 at the input as shown above. You use resistors. This makes the real configuration look more like the figure below which is copied out of a couple of magazine articles by Ray Marston that crib heavily from the data sheet. Unfortunately though he has usefully shown the practical configuration the current flows shown are absolutely wrong for this set-up.
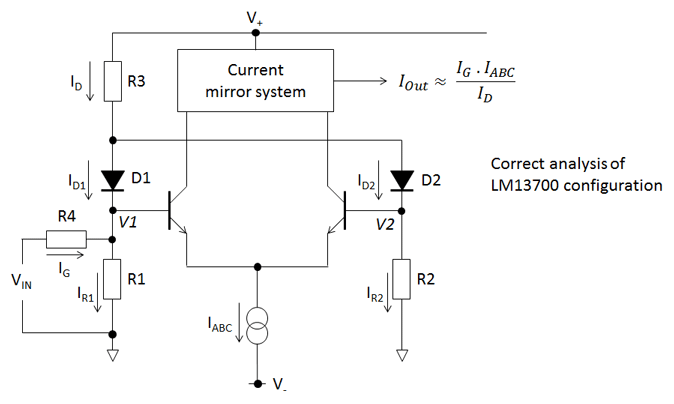
The problem is translating the datasheet theoretical diagram in to the real implementation. An easy thing is to assume (as shown above) that IS is the current through R4 and the rest of the datasheet assumptions then apply leading to IOUT = 2 . IS . IABC / ID. What this overlooks is the role of the ID/2 current sink shown in the datasheet figure. In the data sheet the IS and ID/2 current sources/sinks together force the current in one leg to be ID/2 – IS and this forces the other leg to be ID/2 + IS. When you use a resistor to ground instead of a current sink then the relationship between the current in the two legs changes and the system gain becomes different as well.
Simulation and also careful consideration reveals then when you input a current in one leg in the practical system the effect is to increase the current flowing through both R1 and R2. Let’s try and do some analysis – I have used a new term IG for the input current to remove confusion with IS. I’ve also neglected any currents going in to the base of the transistors that form the differential amplifier. The voltages at the cathode (pointy end) of the two diodes (V1, V2) are approximately equal because a forward biased diode is a rough voltage reference – which means the currents IR1 and IR2 are also approximately equal.
ID1 + ID2 = ID
and ID2 = IR2
and ID1 + IG = IR1
Therefore if IR1 ≈ IR2:
ID2 ≈ ID1 + IG
Or (ID2 – ID1) ≈ IG
and ID1 ≈ ID/2 – IG/2
and ID2 ≈ ID/2 + IG/2
So compared to the Marston diagram the difference in the currents is half that predicted. Assuming the ratio ID1 to ID2 drives the output this makes the system gain:
which fits with roughly the measured results.
So, now do we have the missing equation for the LM13700 gain in its most common configuration? Well the answer is (very) “roughly”! If you are on the ball you will notice that if V1 really was the same as V2 then the differential amplifier would have no differential input and therefore zero output. It is precisely the difference in V1 and V2 that drives the output! Hence the assumption that V1≈ V2 the above derivation is dodgy. All I can say is that from experience and simulation it seems to be OK as long as IG << ID and R1 and R2 are reasonably large. With R1=R2=470 Ohms then the simulated gain is about 12% less than the above formula would suggest. For my applications I always have adjustments to allow the user to set the gain and therefore the above formula is good enough to set the component vaues to give the desired range of adjustment. I suspect if you wrote out the maths properly and did the function expansions you could justify the approximations better and understand exactly how factors like the value of R1 and R2 impact the gain.
From deconstructing what went wrong and fixing my (and it seems others’) faulty assumptions I learnt an incredible amount about the LM13700 operation. What’s the moral here?
1) If a data sheet is obviously written with precision then read it with precision.
2) If there is an interpretation trap then you may not be the only person to fall in to it!
Update (2017)
You can now see the two circuits (datasheet version and “typical” configuration) simulated in the browser here:
http://lushprojects.com/circuitjs/circuitjs.html?startCircuit=ota-gain.txt